How to Calculate Pump Flow Rate: A Step-by-Step Guide
Pump flow rate is a crucial parameter to consider when choosing or specifying a sanitary pump. It tells us how much liquid the pump can move in a certain amount of time and is usually expressed in gallons per minute (gpm), liters per second (l/s), or cubic meters per hour (m³/h).
Why is pump flow rate important?
Let’s say you have a pump that needs to move 100 gallons of water per minute. But the pump can only move 60 gallons per minute. This means that the pump is working at 60% capacity.
Now, let’s say you have another pump that can move 150 gallons per minute. This pump is around 67% utilized if it’s only moving 100 gallons per minute.
As such, knowing how to calculate pump flow rate can help you:
- Choose a pump that is more efficient for your needs
- Assess if your existing system is working efficiently
- Operate your pump at or near its best efficiency point (BEP)
A pump’s BEP is the point at which it produces the most flow with the least amount of power. You don’t want to operate a pump that isn’t powerful enough to meet your needs or one that consumes more energy than necessary.
Worse, failing to operate your pump at its BEP increases the pump’s chance of failure.
Now that we know why pump flow rate is important, let’s learn how to calculate it.
1 – Use Manufacturer-Provided Pump Curves
While there are several ways to calculate pump flow rate, using pump curves is one of the most common. A pump curve goes by several names, including:
- Pump selection curve
- Pump efficiency curve
- Pump performance curve
Pump curves show the relationship between flow rate and head (the maximum height a pump can raise fluid against gravity) for a given pump. They’re provided by pump manufacturers and can be found in the product manual or on the manufacturer’s website.
Check out this pump curve to see what we mean:
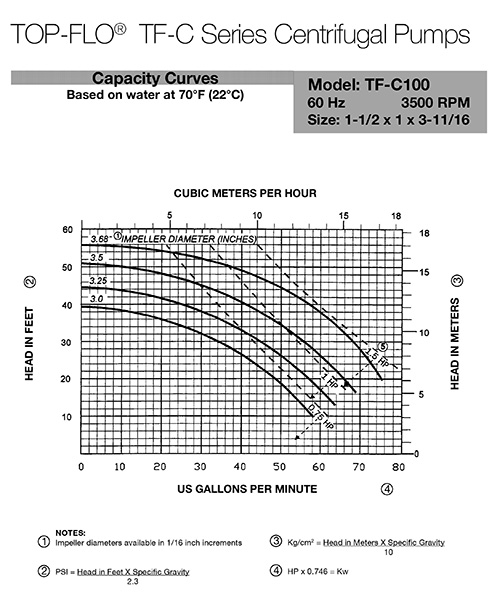
Pump curves include a range of performance metrics, such as:
- Flow rate (measured in gpm, l/s, or m/h)
- Pressure (PSI)
- Head (feet or meters)
- Power consumption (horsepower or kilowatts)
- Impeller trim/diameter (inches)
If you’ve already established some of these metrics, you can use a pump curve to find a pump that meets your desired flow rate. Here’s an example of how you can use pump curves to select a pump.
Say you’re considering a TF-C100 Centrifugal Pump (whose chart is shown above). You’ve picked out the one with a 3.5″ impeller diameter that operates at 1 horsepower.
Assuming that you need the pump to move fluid up 40 feet (head), you’ll:
- Look up your desired head in feet along the chart’s vertical (Y) axis
- Run your finger/ruler straight along the 40-foot mark
- Mark the point where the 3.5” impeller diameter curve interacts with your finger/ruler
- Check the corresponding value on the chart’s horizontal (X) axis
- That value, 40 gallons per minute in our case, is the pump’s flow rate given our set of conditions
It’s worth noting that other factors (discussed towards the end of this article) can influence your pump’s actual flow rate, including:
- Fluid viscosity
- Fluid temperature
- Suction and discharge pipe sizes
Therefore, it’s advisable to get in touch with the pump experts at Sanitary Fittings if you’d like help reading the pump selection curves tailored for your operation.
2 – Use the Affinity Laws

The affinity laws are a set of formulas that describe the relationship between the variables of pump flow rate, head, speed, and power. There are two sets of affinity or pump laws:
- Set 1: Those that treat the impeller diameter as a constant (D = c)
- Set 2: Those that treat the speed variable as a constant (N = c)
Flow Rate Law Where Impeller Diameter Is a Constant
The relevant formula for establishing the flow rate of a specific centrifugal pump when impeller diameter is constant is expressed as: Q₁/Q₂ = (N₁/N₂)
Where Q = flow rate, N = shaft speed, 1 = current or before, and 2 = new or after
By using this formula, we can determine how the flow rate varies when changes are made to the shaft speed. Since the change is directly proportional, a 10% increase in shaft speed will result in a 10% increase in flow rate.
Here’s an example of how you can use this affinity law to calculate pump flow rate.
Say you’re wondering what your pump’s new flow rate, Q₂, would be if the:
- Impeller diameter remained the same
- Current flow rate, Q₁, was 400 gallons per minute
- Current speed, N₁, was 1750 revolutions per minute (rpm)
- New speed, N₂, was 3500 rpm
To calculate the new flow rate:
- Given that impeller diameter is the same, Q₂ = Q₁ (N₂/N₁)
- Substitute the values in the given formula with the figures you have
- Your equation will look like: Q₂ = 400 gpm x (3500 rpm / 1750 rpm)
- Then, Q₂ = 400 gpm x (2)
- Therefore, Q₂ = 800 gpm

Flow Rate Law Where Shaft Speed Is a Constant
You might want to know how your current flow rate would be affected if you used a different impeller diameter while retaining the same shaft speed.
In this case, the flow rate is directly proportional to the impeller diameter. The relevant formula is: Q₁/Q₂ = (D₁/D₂)
Where Q = flow rate, D = impeller diameter, 1 = current or before, and 2 = new or after
For example, assume that you wanted to calculate the new flow rate, Q₂, for your pump given that:
- Shaft speed remained the same
- Current flow rate, Q₁, was 40 gallons per minute
- Current impeller diameter, D₁, was 3.5”
- New impeller diameter, D₂, was 3.68”
Follow these steps:
- Given the shaft speed remains the same, Q₂ = Q₁ (D₂/D₁)
- Substitute the values in the derived formula with the figures you have
- Your equation will look like: Q₂ = 40 gpm (3.68” / 3.5”)
- Then, Q₂ = 40 gpm x (1.05)
- Therefore, Q₂ = 42 gpm
Expert Tip: Changing the impeller diameter will impact its efficiency. While affinity laws can be helpful for calculating how changes in impeller diameter impact pump performance, they’re not always precise.
3 – Calculate the Pump Flow Rate Manually

If you don’t have pump curves, or if the affinity laws aren’t applicable to your situation, it’s still possible to calculate pump flow rate manually.
This method requires you to collect the fluid in a measuring container whose volume is known, and then use the following formula to calculate flow rate: Volume of fluid collected / Time taken
Follow These Steps to Calculate Pump Flow Rate:
- Place your container at the pump’s discharge outlet
- Start the timer when you begin filling the container and stop once it’s full
- Divide the container’s volume by the time it took to fill
For example, if a 20-gallon container took two minutes to fill up, your flow rate would be 20 gallons divided by 2 minutes. The resulting answer of 10 gallons per minute is your pump’s flow rate.
You can also attach a flowmeter to the pump’s discharge piping to measure the flow rate of the fluid passing through your pump. For optimal results, attach the device as close to the pump’s discharge port as possible.
It Pays to Know How to Calculate Pump Flow Rate
Knowing how to calculate pump flow rate will give you confidence when it comes to finding the right pump for your specific application. This knowledge will save you time, money, and energy in the long run.
Check out the table below to get an idea of how different pumps compare in terms of manufacturer-rated flow rates.
| Pump | Rated Flow Rate |
| TF-C100 Centrifugal Pump | 10gpm to 65gpm |
| TF-C114 Centrifugal Pump | 10gpm to 125gpm |
| TF-C216 Centrifugal Pump | 10gpm to 250gpm |
| TF-C218 Centrifugal Pump | 10gpm to 450gpm |
| TF-C328 Centrifugal Pump | 10gpm to 620gpm |
Remember, pump flow rate can be affected by several factors, including:
- Pump size and speed: Larger pumps will move more fluid than smaller pumps, which is why you want an appropriately sized pump for your operation. Similarly, the faster the pump speed (or rpm), the higher its flow rate.
- Liquid temperature, density, and viscosity: Heavier, (denser), and viscous fluids like maple syrup will flow slower than lighter fluids like water. An increase in temperature will generally exponentially reduce a fluid’s viscosity and linearly reduce density.
- Pipe size, length, and bends: Pipes with larger diameters typically have higher flow rates as they have less resistance to flow. Similarly, shorter pipes result in higher flow rates. However, the more bends there are in a pipe, the higher the resistance to flow and the lower the flow rate.
It’s always advisable to consult with a trusted and reliable pump expert to ensure that the sanitary pumps you choose are well suited for your operation.
The team at Sanitary Fittings is committed to providing affordable and high-quality products, coupled with exceptional customer service. You can’t go wrong when you choose Sanitary Fittings, as Lewis discovered:
“Great product, good price, great customer service and easy to order products that ship fast.”
Share on LinkedIn:


